איך בוטי פוקר משתמשים במתמטיקה כדי לשלוט במשחק

כמובן, פוקר הוא משחק של מיומנות, אסטרטגיה, ומעל הכל, מתמטיקה. בעוד שבני אדם מסתמכים על אינטואיציה, ניסיון ולעיתים גם על קצת מזל, בוטי פוקר פועלים ברמה שונה לחלוטין. מצוידים במודלים מתקדמים של הסתברות, אלגוריתמים מתמטיים מתקדמים ועקרונות של תורת המשחקים, הבוטים יכולים לחשב את הסיכויים המדויקים תוך כדי חיזוי מהלכי היריבים ואופטימיזציה של כל החלטת הימור בזמן אמת.

אבל איך בדיוק בוטי פוקר מבצעים את החישובים המתמטיים כדי לשלוט במשחקים? המאמר הבא בוחן את המודלים המתמטיים המרכזיים שמאחורי בוטי הפוקר, איך הם מחשבים סיכויים, ואיך האלגוריתמים המשופרים הללו מצליחים לעיתים קרובות להתעלות על יריביהם האנושיים.

סקירה של המתמטיקה שמאחורי בוטי הפוקר

בבסיסו של כל בוט פוקר מוצלח עומדת שילוב של מודלים מתמטיים שונים, שנכנסים לפעולה כדי להעריך את המצב בשולחן, לחשב את ההסתברויות ולבצע את הפעולה האופטימלית לאחר מכן. דוגמאות כוללות:

• תורת ההסתברות: הערכת הסיכויים לתוצאה סבירה.
• ערך צפוי (EV): לבחירת פעולות רווחיות לטווח הארוך.
• מודלים של GTO: מבטיחים שהמשחק לא יהיה ניתן לניצול.
• סימולציות מונטה קרלו: הרצת סימולציה של אלפי תוצאות משחק אפשריות.
• הסקה בייסיאנית: התאמת שיטות על בסיס תצפיות על דפוסי ההימורים של היריבים.

על ידי שילוב של היבטים אלו של מתמטיקה, בוט פוקר יכול, בתוך אלפיות שנייה, למיין מיליוני מהלכים ותוצאות אפשריות ולתכנן אסטרטגיות מתוך המידע.

1. מודלים של הסתברות: חישוב סיכויים ו-outs

כל תהליכי קבלת ההחלטות שמבצעים בוטי פוקר מבוססים על מודלים של הסתברות. מהעלאות לפני הפלופ ועד קריאות בריבר, הכל כולל חישובים מדויקים לגבי outs, סיכויי קופה והסתברויות זכייה.

איך בוטי פוקר משתמשים במודלים של הסתברות:

• חישוב outs: הבוטים סופרים את ה-outs, כלומר הקלפים שיכולים לשפר את היד שלהם.
• סיכויי זכייה: הנוסחה הבאה מיושמת:

סיכויי זכייה=Outs×4 (אחרי הפלופ)​/קלפים שנותרו

• סיכויי קופה: הם שוקלים את גודל הקופה בכל נקודת זמן ואת גודל ההימור שהם יצטרכו לקרוא כדי לקבוע אם הקריאה תהיה רווחית.

דוגמה: הקופה היא $100, הבוט צריך לקרוא הימור של $20, כך שסיכויי הקופה הם 5:1. אם הסיכוי של הבוט לזכות גבוה מזה, הוא קורא.

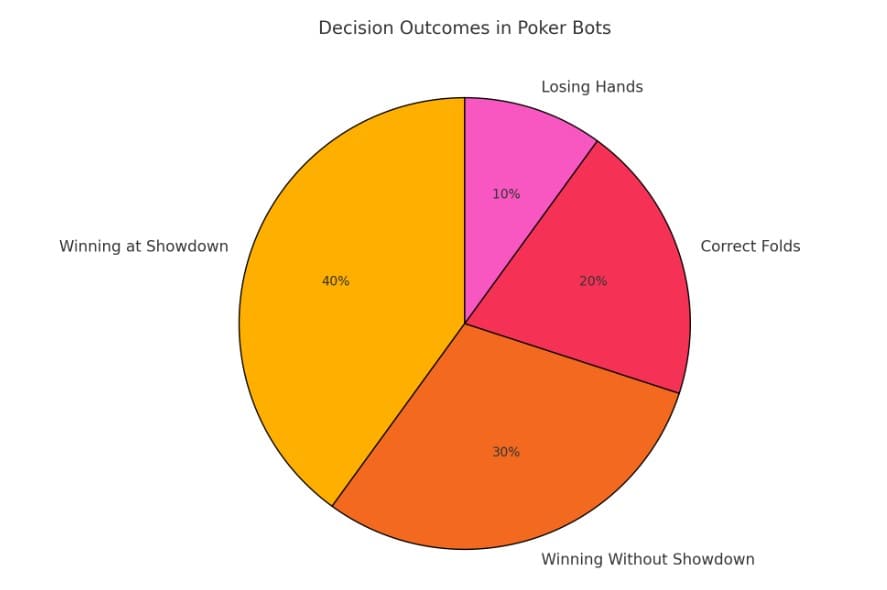
2. ערך צפוי: למקסם רווח לטווח הארוך

ערך צפוי בפוקר הוא דרך להגדיר כמה מהלך מסוים יניב בממוצע לאורך זמן. בוטי פוקר מבססים את האסטרטגיות שלהם על הבטחת כל פעולה שתניב להם EV חיובי: להמר, לקרוא ולקפל.

נוסחת EV

EV=(הסתברות זכייה×סכום זכייה)−(הסתברות הפסד×סכום הפסד)

דוגמה:

לדוגמה, אם לבוט יש 70% סיכוי לזכות בקופה של $200 על ידי כניסה לאול-אין עם הימור של $100, ה-EV שלו ייראה כך:

EV=(0.7×200)−(0.3×100)=140−30=110

מכיוון שה-EV חיובי, +$110 אומר שהבוט יכול להיכנס לאול-אין.

3. GTO: תורת המשחקים האופטימלית: מודלים של משחק מושלם

GTO פשוט אומר תורת המשחקים האופטימלית—אסטרטגיה למשחק פוקר שמטרתה לשמור על הבוט במצב שאינו ניתן לניצול. האגרסיביות מאוזנת מול ההגנה בניסיון או רצון לשמור על הבוט קשה לניבוי.

איך GTO עובד:

• טווחים מאוזנים: הבוטים מאזנים הימורי ערך ובלופים בצורה מושלמת.
• עקרון האדישות: יריב צריך להיות אדיש בין קריאה לקיפול מול הבוט.

דוגמה:

אם הבוט מבלף 33% מהזמן ומהמר על ערך ב-67% מהזמן בריבר, יריב לעולם לא ידע אם הוא מתמודד מול יד חזקה או בלוף. זה הופך אסטרטגיות נגד לכמעט בלתי אפשריות.

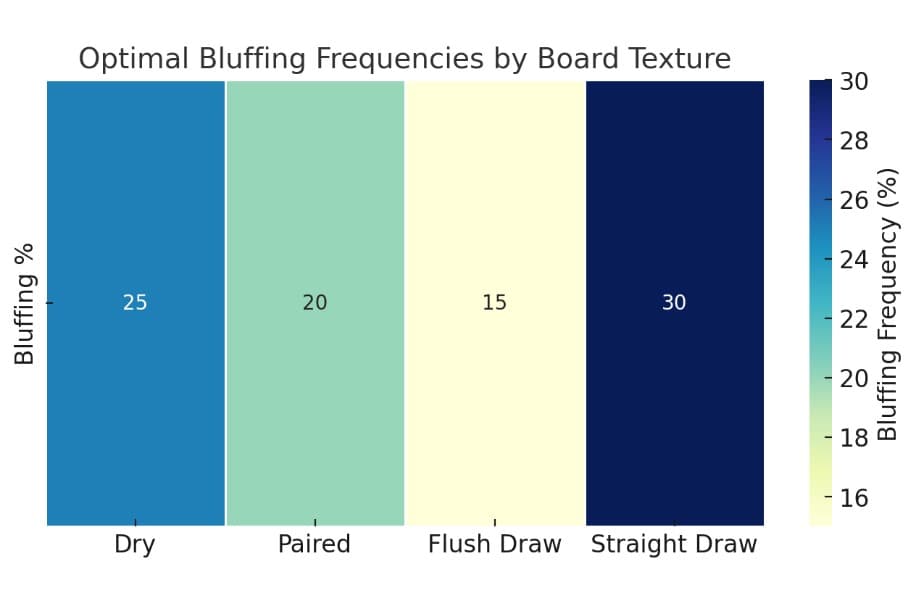
4. סימולציית מונטה קרלו: כל דרך אפשרית

סימולציות מונטה קרלו שבהן משתמשים בוטי פוקר מעריכות את ערך היד על ידי סימולציה של מיליוני תוצאות משחק אפשריות. זו דרך מצוינת להעריך את ההסתברות לזכייה על ידי בדיקת כל הריצות האפשריות.

איך זה עובד:

• היא משתמשת במיליוני סימולציות משחק אקראיות כדי לתעד את תדירות הזכייה של ידיים מסוימות.
• היא מריצה סימולציות שונות כדי לחשב את התפלגויות ההסתברות.

דוגמה:

כך, אם לבוט יש A♥ K♣ מול טווח של יריב, הוא יחשב אחוז זכייה מדויק דרך סימולציות של פלופים, טרנים וריברים אפשריים אלף פעמים.

5. הסקה בייסיאנית: התאמה ליריבים

בוטי פוקר לא מסתמכים רק על מתמטיקה סטטית – הם משתמשים בהסקה בייסיאנית כדי להתאים אסטרטגיות על בסיס דפוסי הימורים שנצפו. מודל הלמידה האדפטיבי הזה מעדכן הסתברויות ככל שמידע חדש הופך זמין.

נוסחת עדכון בייסיאני:

הסתברות פוסטריורית=סבירות×הסתברות קודמת​/ראיה

דוגמה:

הבוט מעדכן את ההסתברויות הקודמות שלו לגבי רמת האגרסיביות של שחקן כאשר יריב אחד מבצע 3-bet בתדירות גבוהה לפני הפלופ, וכך מתאים את האסטרטגיה שלו להגנה רבה יותר עם ידיים חלשות.

מתמטיקה מתקדמת מאחורי בוטי פוקר

מעבר לרעיונות שהוזכרו, בוטי פוקר משתמשים במנגנונים מתוחכמים עוד יותר, כמו הבאים:

• רשתות נוירונים: זה כולל למידה עמוקה לזיהוי דפוסים.
• למידת חיזוק: בוטים ילמדו דרך משחק עצמי על ידי ביצוע טעויות.
• מודלים של שיווי משקל נאש: לאסטרטגיות טובות מובטחות במשחקי ראש-בראש ובטורנירים.

למרות שמושגים מתמטיים דומים יכולים להיות מיושמים על ידי שחקנים אנושיים, מדובר במיליוני חישובים בשנייה ללא טעויות רגשיות כמו טילט או שיפוט שגוי של יריבים. זו הגישה המתמטית המונעת על ידי נתונים שממקמת אותם לפני רוב היריבים האנושיים כמעט בכל סביבה מקוונת.

סיכום: מתמטיקה כמפתח להצלחת בוטי פוקר

אבל הסוד של כל בוט פוקר מצליח מבוסס בעיקר על מתמטיקה: מודלים של הסתברות, חישוב ערך צפוי, אסטרטגיות GTO וסימולציות מונטה קרלו—הבוטים הופכים את זה למשחק של מספרים, משחק שהם כמעט ולא מפסידים בו.

אולי זה מעודד לדעת איך המודלים הללו עובדים; עבור שחקנים אנושיים, ניתן לשפר זאת גם כן על ידי שימוש בעקרונות דומים ללא כוחות החישוב של בוט פוקר.